در این مقاله از راکت، چگونگی الگوریتمهای سرچ باینری و نحوه پیادهسازی آن را در پایتون میآموزید.
و به صورت خاص موارد زیر را یاد میگیرید:
- نحوه کار الگوریتمها در پشت صحنه برای پیداکردن عناصر هدف
- نحوه اجرای خط به خط کد پایتون
- چرا این الگوریتم نسبت به جستجوی خطی کارآمدتر است
- و موارد دیگر ...
بیایید شروعکنیم!
معرفی جستجوی دوتایی (باینری)
این الگوریتم برای پیداکردن عناصر در یک ترتیب توالی استفاده میشوند (برای مثال: یک لیست، رشته، tuple)
ملزومات
برای استفاده از الگوریتم جستجوی دوتایی برای یک دنباله، دنباله کنونی باید در یک ترتیب صعودی ذخیره شود. درغیر اینصورت، الگوریتم جواب درست را پیدا نخواهد کرد و اگر هم پیدا کند اتفاق محض خواهد بود.
نکته: میتوانید دنباله را قبل از جستجوی دوتایی با یک الگوریتم قوی که نیازهای شما را پوشش میدهد مرتبسازی کنید.
ورودی و خروجی
الگوریتم (بهعنوان یک تابع اجرایی) نیاز به این دادهها دارد:
دنباله ترتیبی عناصر (بعنوان مثال: لیست و رشته،tuple )
هدف عناصر که ما بهدنبال آن هستیم.
که بستگی به پیوست عناصری که شما به دنبال آن هستید دارد. اگر عناصر را نیابید ۱- بازگردانده میشود.
کارآمدی
در مقایسه با جستجوی لینر (خطی) بسیار کارآمدتر است (برای جستجو عنصری به صورت تک به تک از ابتدا) چون ما میتوانیم درهر مرحله نیمی از لیست را نادیده بگیریم.
بیایید با این الگوریتم بیشتر آشنا شویم.
دید بصری
ما میخواهیم جستجوی باینری الگوریتم را در این لیست بکار بگیریم:

نکته: توجهکنید که لیست هماکنون مرتب شده است و شامل شاخصهای بصری است.
هدف
میخواهیم شاخص عدد صحیح ۶۷ را پیدا کنیم.
فاصله
بیایید تظاهر کنیم که ما الگوریتم هستیم. چگونه فرآیند را شروع کنیم؟
ما با انتخاب دو باند فاصله که میخواهیم جستجو کنیم، شروع میکنیم. میخواهیم کل لیست را جستجو کنیم بنابراین ما شاخص ۰ را بعنوان باند کمینه و شاخص ۵ را بهعنوان باند بیشینه انتخاب میکنیم.
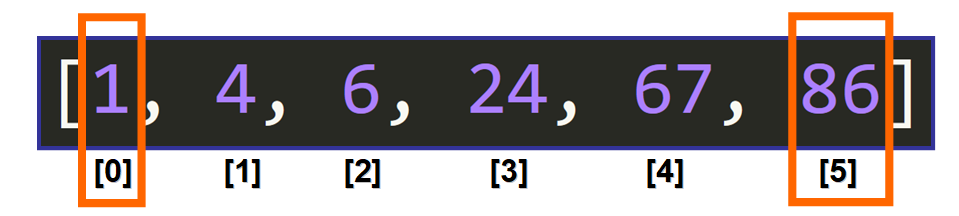
عناصر میانه
حالا میخواهیم شاخص میانه عناصر را در این فاصله پیدا کنیم. ما این کار را با جمع باند کمینه و بیشینه و تقسیم نتیجه بر عدد ۲ با استفاده از گردسازی به صورت عدد صحیح انجام میدهیم (یعنی نتیجه به صورت عدد صحیح بیان میشود و قسمت اعشار گرد میشود).
در این حالت ۲//(۰+۵) میشود ۲ چون نتیجه ۲.۵ است و تقسیم عدد صحیح، بخش اعشاری را گرد میکند.
بنابراین عنصر میانه در شاخص ۲، و عنصر میانه روی شاخص ۶ میشود:
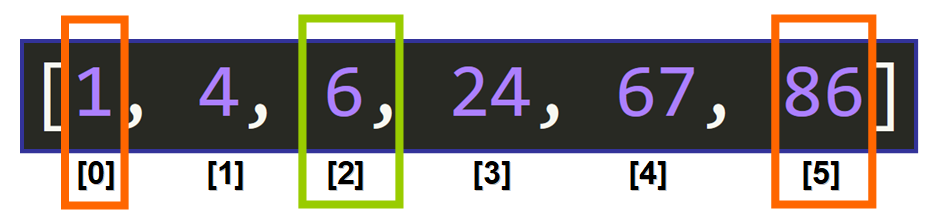
مقایسات
حالا ما باید مقایسه بین عنصر میانی با عنصر هدف را برای اینکه بدانیم در مرحله بعدی به چه چیزی نیاز خواهیم داشت، انجام دهیم.
ما در قبل پرسیدیم:
آیا عنصر میانه برابر با عنصری است که ما میخواهیم به دنبالش بگردیم؟
6 == 67 # Falseنه! اشتباهاست.
خب پس میپرسیم:
آیا عنصر میانه بزرگتر از عنصری است که ما به دنبالش هستیم؟
6 > 67 # Falseنه! نیست.
بنابراین عنصر میانه کوچکتر از عنصری است که ما به دنبالش هستیم.
6 < 67 # Trueنادیدهگرفتن عناصر
از آنجا که لیست هماکنون مرتبسازی شده است، که نشانگر یک نکته به شدت مهم است که میگوید: ما میتوانیم نیم کمینه لیست را نادیده بگیریم چون میدانیم که تمام عناصری که قبل از عنصر میانه میآیند، کوچکتر از عنصری هستند که ما به دنبالش هستیم. بنابراین عنصر هدف ما در آنجا قرار ندارد.
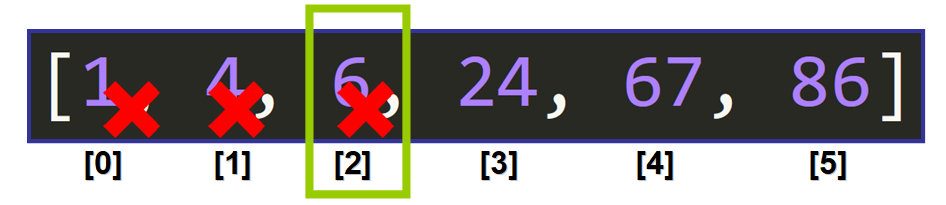
دوباره شروع کنید! یک باند دیگر انتخاب کنید.
بعدش چیکار کنیم؟ ما این عناصر را نادیده میگیریم و دوباره کار را از اول شروع میکنیم.
ما باید باندهایی برای شروع دوباره انتخابکنیم. اما دقت کنید که باند بیشینه به همان صورت باقی مانده است و باند کمینه یا پایینی است که تغییر کرده است.
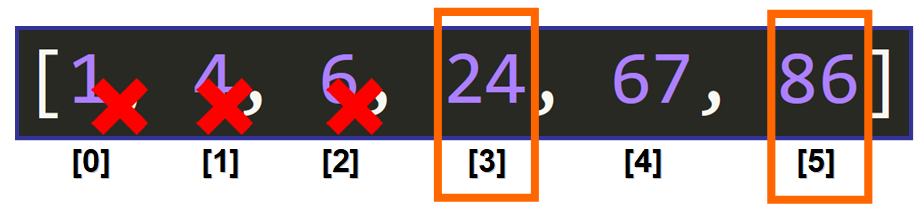
بخاطر این است که عناصری که ما به دنبال آن هستیم میتوانند در بخش بیشینه دیگر لیست باشند. باند بالایی دستنخورده میماند و باند کمینه تقلیل مییابد. جایی که میتوانیم عنصر مورد نظر خود را پیدا کنیم.
نکته: اگر عنصر میانه، بزرگتر از عنصری که ما به دنبالش هستیم باشد باند بیشینه باید تغییر کند و باند کمینه دستنخورده باقی میماند. با این روش میتوانیم نیمی از بخش بیشینه لیست را نادیده بگیریم و جستجو را در نیمه کمینه ادامه دهیم.
عنصر میانه
اکنون ما نیاز داریم تا شاخص عنصر میانه را با جمع باند کمینه به باند بیشینه و تقسیم نتیجه بر ۲ (حاصل را به صورت عدد صحیح گرد کنید) به دست آوریم.
نتیجه ۲/(۳+۵) میشود ۴، بنابراین عنصر میانه در شاخص ۴ واقع شدهاست و عدد میانه ۶۷ است.
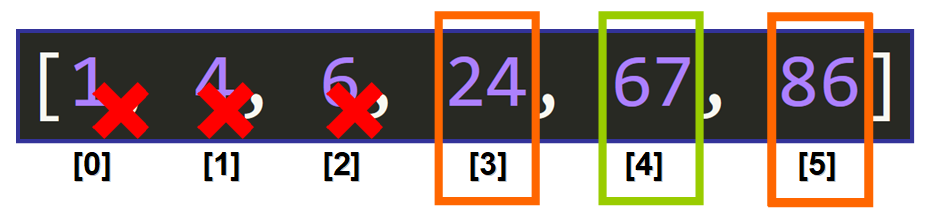
مقایسات
آیا عنصر میانه برابر با عنصری است که ما بهدنبالش هستیم؟
67 == 67 # Trueبله، هست! بنابراین ما عنصر را در شاخص ۴ پیدا کردهایم. مقدار ۴ برگشت میخورد و الگوریتم با موفقیت کامل میشود.
نکته: اگر عنصری پیدا نشد، فرآیند تا زمانی که فاصله اعتبار خود را از دست دهد ادامه مییابد. اگر عنصر در کل لیست پیدانشد ۱- بازگردانده میشود.
نگاهی به کد الگوریتم
حالا ما میتوانیم یک دید بصری از چگونگی کار الگوریتم در پشت صحنه داشته باشیم. بیایید با تجزیه و تحلیل خط به خط پایتون این کار را به اتمام برسانیم.
def binary_search(data, elem):
low = 0
high = len(data) - 1
while low <= high:
middle = (low + high)//2
if data[middle] == elem:
return middle
elif data[middle] > elem:
high = middle - 1
else:
low = middle + 1
return -1سرتیتر
ما در اینجا تابع را میبینیم:
def binary_search(data, elem):این تابع دو آرگومان میگیرد:
- دنباله مرتبسازی شدهی عناصر ( برای مثال: لیست و رشته و tuple)
- عناصری که میخواهیم پیدا کنیم.
کدهای اولیه
خط بعدی مرزهای پایین و بالایی اولیه را تعیین میکند.
low = 0
high = len(data) - 1باند کمینه آغازین شاخص ۰ است و باند بیشینه آغازین آخرین شاخص دنباله است.
حلقه
ما فرآیند را تاجاییکه ورود معنیداری وجود داشته باشد ادامه میدهیم. جایی که باند کمینه کوچکتر و یا برابر با باند بیشینه است.
while low <= high:نکته: به یاد داشته باشید که باندها شاخصها هستند.
عنصر میانه
درهر تکرار، ما نیاز داریم که شاخص عنصر میانه را پیدا کنیم. برای انجام این کار ما باید باند بالایی و پایینی را باهم جمع کنیم و نتیجه را بر ۲ تقسیم و عدد حاصل را به صورت عدد صحیح گرد کنیم.
middle = (low + high)//2نکته: ما از تقسیم عدد صحیح درمواردی که لیست یا فاصله حاوی اعداد زوج باشند، استفاده میکنیم. بهعنوان مثال اگر لیست عنصر ۶ داشته باشد و ما از تقسیم عدد صحیح استفاده نکنیم، میانه نتیجهی کسر ۲/(۰+۵) می باشد که جواب آن ۲.۵ است. یک شاخص نمیتواند از نوع float باشد، بنابراین ما با استفاده از // قسمت اعشاری را گرد میکنیم و عنصر را در شاخص ۲ انتخاب میکنیم.
مقایسات
با این شرایط، ما آنچه را که برای بازسازی مقدار عنصر میانه data[middle] باید انجام دهیم مشخص نمودیم. ما این را با عنصر هدفی که ما به دنبالش بودیم مقایسه میکنیم.
if data[middle] == elem:
return middle
elif data[middle] > elem:
high = middle - 1
else:
low = middle + 1ما سه گزینه داریم:
- عنصر میانه برابر با عنصری است که ما بهدنبالش هستیم که در نتیجه ما فوراً به شاخص بازمیگردیم چون عنصر را یافتهایم.
if data[middle] == elem:
return middle- اگر عنصر میانه بزرگتر از عنصری باشد که ما بهدنبال آن هستیم، باید دوباره باند بالایی را تعیین کنیم چون ما میدانیم که عنصر هدف کمتر از نصف لیست است.
elif data[middle] > elem:
high = middle - 1- دیگر آنکه، تنها گزینهای که باقیمانده است این میباشد که عنصر میانه کوچکتر از عنصری است که ما بهدنبالش هستیم، بنابراین ما دوباره باند کمینه را تعیین میکنیم چون ما میدانیم که عنصر میانه در بالای نیمی از لیست قرار دارد.
else:
low = middle + 1عنصر پیدا نشد!
اگر حلقه بدون یافتن عنصر کامل شود مقدار ۱- بازمیگردد.
return -1و ما در آخر پیادهسازی نهایی الگوریتم جستجوی باینری را داریم:
def binary_search(data, elem):
low = 0
high = len(data) - 1
while low <= high:
middle = (low + high)//2
if data[middle] == elem:
return middle
elif data[middle] > elem:
high = middle - 1
else:
low = middle + 1
return -1موارد استثنایی
این ها مواد خاصی هستند که شما شاید در شروع کار خود با این الگوریتم با آنها مواجه شوید:
عناصر تکراری
اگر عنصری که بهدنبالش هستید در دنباله تکرار شده است، بازگشت شاخص بستگی به تعداد عناصر و عملیات روی دنباله ادامه پیدا خواهد کرد.
>>> >>> b = [2, 2, 3, 6, 7, 7]
>>> binary_search(b, 7)
4عنصر پیدانشد!
اگر هیچ عنصری پیدا نشود ۱- بازگرداننده میشود.
>>> b = [2, 2, 3, 6, 7, 7]
>>> binary_search(b, 8)
-1دنباله خالی
اگر توالی خالی باشد ۱- بازگرداننده میشود.
>>> b = []
>>> binary_search(b, 8)
-1دنباله نامرتب
اگر دنباله نامرتب باشد، جوابی که پیدا شده است درست نخواهد بود. یافتن شاخص صحیح یک اتفاق تصادفی است و میتواند در نتیجهی ترتیب عناصر در دنباله و عملیات توالیها توسط الگوریتم به نمایش درآید.
مثال زیر نتیجه صحیح را باز میگرداند:
>>> b = [5, 7, 3, 0, -9, 2, 6]
>>> binary_search(b, 6)
6اما این یکی باز نمیگرداند:
>>> b = [5, 7, 3, 0, -9, 2, 10, 6]
>>> binary_search(b, 6)
-1نکته: درمورد اینکه چرا در مثال اول بازگشت نتیجه صحیح رخ میدهد، فکر کنید!
یک مثال پیچیدهتر
حالا که شما با الگوریتم و نحوه کار پایتون بیشتر آشنا شدید ما در اینجا یک مثال پیچیدهتر میآوریم:
ما میخواهیم شاخص عنصر ۴۵ را در این لیست با استفاده از جستجوی باینری پیدا کنیم:

تکرار اول
باند کمینه و بیشینه انتخاب شدند:

عنصر میانه ۲۶ انتخاب شد:

اما عنصر میانه (۲۶) عنصری که ما به دنبالش هستیم نیست. کوچکتر از ۴۵ است:
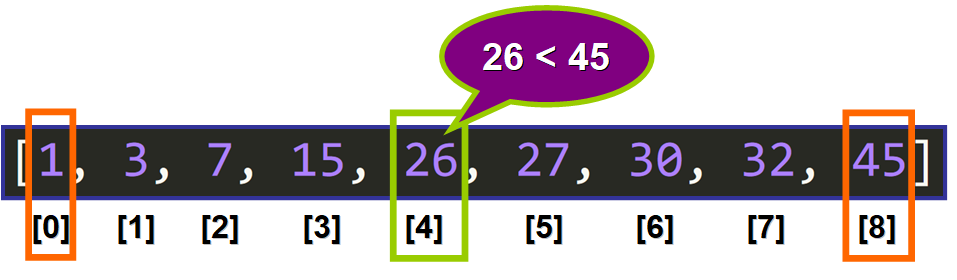
تکرار دوم
بنابراین ما میتوانیم تمام عناصری که کوچکتر از عنصر میانه هستند نادیده بگیریم و یک باند جدید انتخابکنیم. در باند جدید کمینه ۲۷ است که این عنصر در سمت راست عنصر میانه قبلی واقع شده است.

نکته: به یاد داشته باشید که لیست هماکنون مرتب است.
عنصر میانه جدید ۳۰ انتخاب شد:

عنصر میانه (۳۰) عنصری نیست که ما بهدنبالش هستیم، کوچکتر از ۴۵ است:
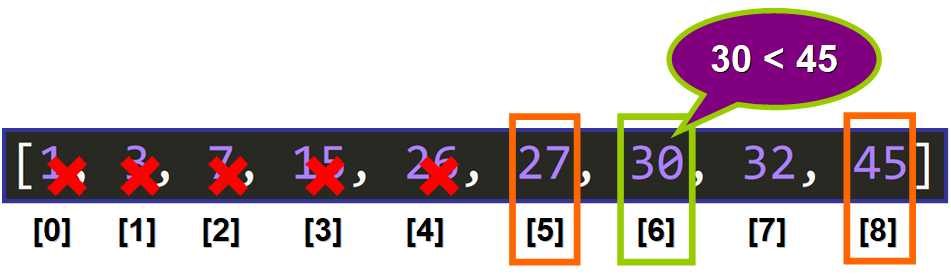
تکرار سوم
ما میتوانیم عناصری که کوچکتر و یا برابر با ۳۰ هستند را نادیده بگیریم، که تاکنون نادیده گرفته نشدهاند. باند کمینه به ۳۲ تغییر میکند:

در اینجا ما یک مورد جالب داریم: عنصر میانی یکی از باندهای فاصله کنونی است چون: نتیجه ۲//(۷+۸) میشود ۷.

عنصر میانی ۳۲ عنصری نیست که ما به دنبالش هستیم (۴۵)، از آن چیزی که ما میخواهیم کوچکتر است.
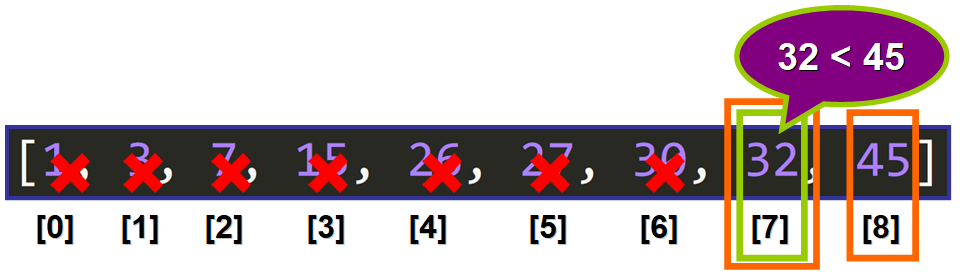
تکرار چهارم
ما میتوانیم عناصری که کوچکتر و یا مساوی با ۳۲ هستند (آنهایی که تاکنون نادیده نگرفتهایم) را نادیده بگیریم.
اینجا ما یک مورد بسیار جالبتر داریم: فاصله فقط یک عنصر دارد.

نکته: این فاصله معتبر است چون ما برای آن while high <= low: نوشتیم، که شامل فواصلی است که شاخص باند کمینه برابر با شاخص باند بیشینه است.
عنصر میانی تنها عنصر در فاصله است چون ۲//۸+۸ میشود ۸. بنابراین شاخص عنصر میانه ۸ است و عنصر میانه ۴۵ است.
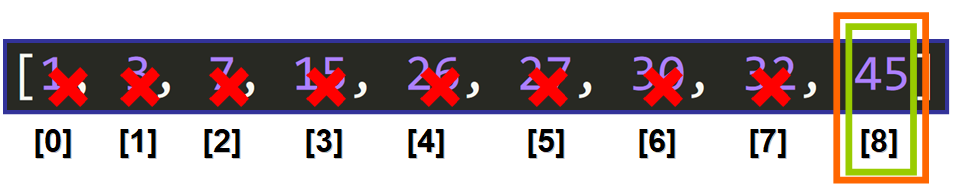
حالا عنصر میانه عنصری است که ما به دنبال آن بودیم، یعنی ۴۵ است:
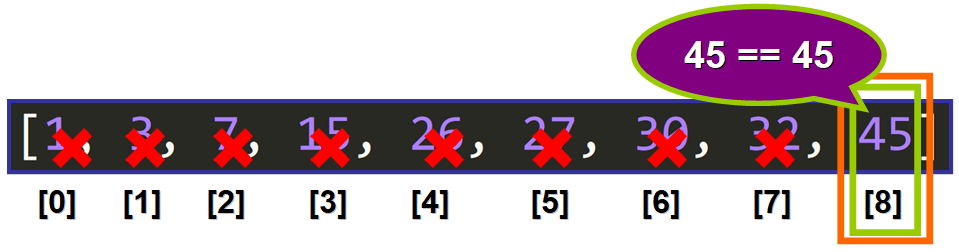
بنابراین مقدار ۸ (شاخص) بازمیگردد.
>>> binary_search([1, 3, 7, 15, 26, 27, 30, 32, 45], 45)
8تمرین اضافی
اگر شما مایل هستید که کمی تمرین اضافه با این الگوریتم انجام دهید، سعیکنید چگونگی کار الگوریتم در پشت صحنه را هنگامیکه آن را به این لیست افزودید تا عدد صحیح ۹۰ را پیدا کنید، توضیح دهید.
[5, 8, 15, 26, 38, 56]- مرحله به مرحله چه چیزی اتفاق میافتد؟
- چه مقداری بازگشت میکند؟
- آیا عنصر پیدا میشود؟

در حال دریافت نظرات از سرور، لطفا منتظر بمانید
در حال دریافت نظرات از سرور، لطفا منتظر بمانید